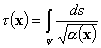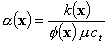|
|
|
|
|
|
|
|
|
|
·
Past Record
download
·
Proposed Research
Following is a brief discussion of some of our ongoing research activities. This is not meant to be a comprehensive list. The purpose is to provide sufficient detail for the reader to have a general understanding of our activities. We will update this page from time to time.
We want to build on our success on streamline-based history matching and generalize its applicability to a much wider class of reservoir problems using conventional finite-difference simulators. These include three-phase flow, corner-point geometry and unstructured grids. A unique feature of streamline models is their ability to analytically compute the sensitivity of the production data with respect to reservoir parameters using a single flow simulation. These sensitivities define the change in production response because of small changes in reservoir parameters and are a critical aspect of any production data integration algorithm. We utilize a novel approach to history matching finite difference models that combines the advantage of the streamline models with the versatility of finite-difference simulation. The goal here is to use the streamline-derived sensitivities in a finite-difference simulator. Thus, we will first generate streamlines using the velocity field from a conventional finite difference simulator. In particular, the use of commercial simulators such as ECLIPSE or VIP will allow us to preserve the generality of the approach including corner point geometry, faulted systems and three-phase flow. The streamlines are used to efficiently compute the parameter sensitivities that are then utilized to update the reservoir model via the generalized travel time inversion. The updated model is then used in the finite-difference simulation to predict reservoir performance and the process is repeated until a satisfactory history match is obtained. The underlying basis here is that the parameter sensitivities during history matching of the finite-difference models do not have to be ‘exact’; streamline-derived approximate sensitivities may suffice for most situations resulting in a significant speed-up in computation. The sensitivity computations rely on the recently proposed predictor-corrector approach to streamline simulation (Osako et al., 2003). Using the predictor corrector approach, we can rigorously account for compressibility and solution gas effects in three-phase flow. Our approach will be suitable for both ‘assisted’ and ‘automatic’ history matching. Our preliminary results indicate that the proposed approach can be orders of magnitude faster than commercial history matching programs for finite-difference simulators.
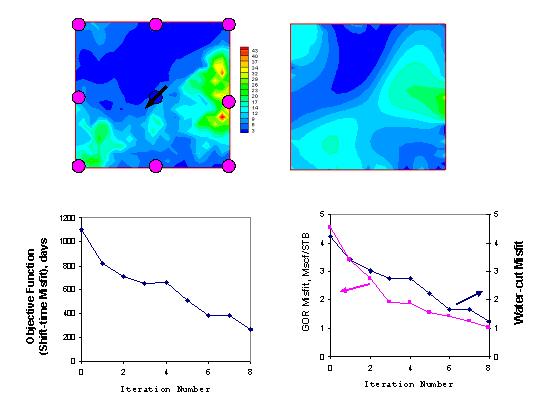
Figure: History matching 3-phase finite-difference model for a nine-spot heterogeneous case: (a) reference permeability, (b) final permeability, (c) objective function (shift-time) misfit reduction for joint inversion of gas/oil ratio and water-cut data, and (d) GOR and water-cut amplitude misfit reduction.
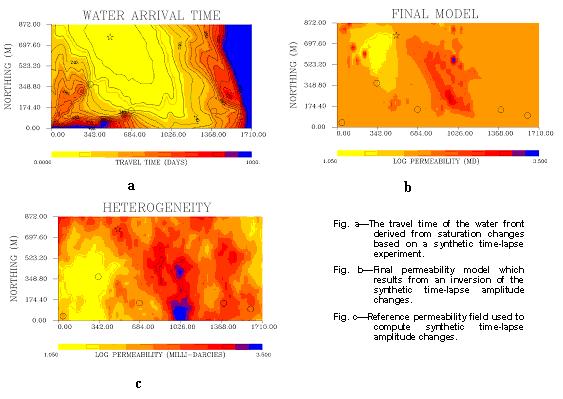
Time-lapse seismic is maturing as a technology and is being increasingly used for reservoir management and monitoring purposes. The guidelines for its application are also becoming clear based on the industry experience. The methodology is advancing rapidly and new techniques are under development which allow for discrimination between pressure and fluid saturation changes over time. To date, time-lapse seismic has primarily served as a monitoring tool. That is, time-lapse seismic observations are used to map changes in reservoir saturation and pressure. The next logical step is to use time-lapse seismic data to characterize the reservoir, to infer reservoir permeability and porosity distribution. The additional information provided by the time-lapse data will result in more accurate predictions of the performance of future production efforts. Currently, there have been few attempts at formal reservoir characterization using 3D time-lapse observations. By formal reservoir characterization, we mean some manner of inversion of the time-lapse field data along with field production history for reservoir flow properties. Time-lapse reservoir characterization is hampered by computational difficulties. Typically, finding a reservoir model which is compatible with a set of saturation and pressure changes derived from the time-lapse data requires a significant number of reservoir simulations. Because each reservoir simulation may take hours, if not days, of CPU time on a workstation, formal inversion can be prohibitively expensive. Recently
streamline-based flow simulation models have demonstrated significant
potential in integrating time-lapse seismic data into high-resolution
reservoir models. The streamline approach has relied on computing and
matching "travel time" of fluid fronts at the wells and can be
naturally extended to directly relate time-lapse images of a multiphase
front to reservoir properties. In particular, saturation, porosity, and
pressure variations in the reservoir will induce changes in seismic
attributes such as "amplitude" or the "travel time". These changes can
be incorporated into the streamline-based history matching using
appropriate rock physics models. The result will be interwell
saturation maps that are constrained by both production and seismic
data. A key advantage of our approach will be its computational
efficiency that makes it ideally suited for large-scale field
applications. Our preliminary applications at the Bay Field in the
One promising new development is the use of time-lapse seismic data to discriminate between pressure and saturation changes within a reservoir utilizing amplitude variations with offset (AVO) analysis. The estimates of pressure changes may be used to estimate permeability variations in the reservoir. The work is motivated by the coupled inversion of surface deformation and pressure data as proposed by Vasco et al. (2001). The approach is appealing because the associated inverse problem is linear and can potentially avoid much of the difficulties associated with existence of local minimum, lack of convergence and problems in model assessment. Furthermore, imaging pressure changes makes it possible to infer permeability in regions of the reservoir which have not yet undergone saturation changes. Thus, we can image permeability ahead of a propagating multi-phase front and predict the movement of the front.
Integration
of pressure data into reservoir models is still a time-consuming
proposition. In spite of several new developments in the area of
efficient sensitivity computation, typically the computational expense
depends on the number of parameters and/or the number of data points.
With the permanent down-hole pressure sensors becoming more common, the
amount of data collected can be overwhelming. In addition to
computational efficiencies, there are issues related to data
redundancy. To circumvent the problem, we recently utilized an
asymptotic solution to the diffusivity equation to incorporate
transient pressure response to reservoir models using trajectory-based
methods (Vasco et al., 2000; Datta-Gupta et al., 2001). Asymptotic
approaches in seismology have relied on defining ray paths or
trajectories associated with wave-fronts. For fluid flow modeling, such
trajectories can often be identified with streamlines. The trajectory,
described by the ray equations, is the path taken by the first-arriving
pressure transient. The square root of the travel time from the source
or injection well to an observation well, t(x),
is given by a line integral along this trajectory (also called a
‘diffusive time of flight’),
In this expression S is the trajectory
from the source to the observation point α(x)
is the diffusivity given by the ratio of
permeability to
reservoir storage,
which is a function
of distance r along the flow path. Using the
relationship given above, we can perform transient pressure travel time
tomography. That is, we can utilize concepts such as back-projection
and sparse matrix methods to construct an efficient algorithm for
mapping arrival time anomalies into lateral variations of k(x) (see figure
below). It was also shown that the diffusive time of flight provides us
with drainage volumes and drainage areas associated with primary
production under very general conditions and allows us to visualize
reservoir flow patterns.
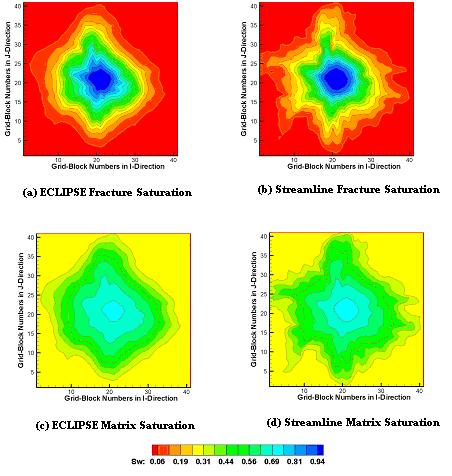
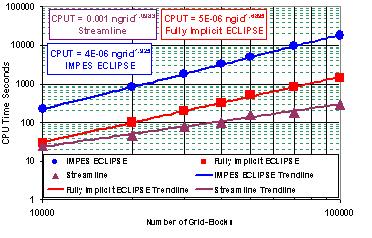
Fractured reservoirs pose some unique challenge because these reservoirs primarily act as dual interacting continua with the fracture systems proving the main fluid flow path and the matrix system providing the fluid storage. Recently we have developed a streamline simulator for dual porosity dual permeability systems and extensively tested the simulator against commercial finite-difference simulators for fractured reservoirs. For waterflood applications, the results from the streamline simulator were in close agreement with the finite-difference simulator. However, unlike the finite-difference simulator, the streamline model exhibited minimal effects of numerical dispersion. Further, the CPU time for the streamline simulator showed a linear scaling with respect to the number of grid blocks making it ideally suited for large-scale field applications. The unique aspect of the dual permeability formulation is the introduction of two sets of co-ordinate transformation: one based on the time of flight for matrix and a second one based on the time of flight for fractures. The cross-flux between the matrix and the fracture system is accounted for via a predictor-corrector approach. The dual permeability approach allows us to explicitly account for flow in the matrix. In the absence of significant matrix flow, the fracture velocity becomes the total velocity which is a conserved quantity. The approach simplifies to a dual porosity formulation.
Figure: Comparison between the DPDP streamline simulator and the DPDP ECLIPSE in terms of water saturation after 1000 days, heterogeneous nine-spot case, imbibition process.
Figure: Scaling of CPU time: DPSP ECLIPSE vs. streamline
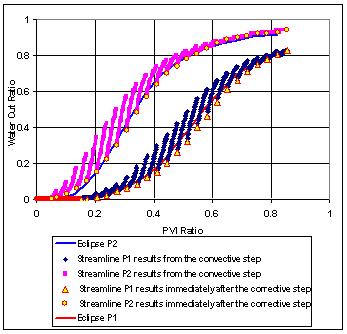
Recently we proposed a predictor-corrector formulation for streamline approach that allows us to include transverse flux during streamline simulation (Osako et al., 2003). The underlying idea is to solve for the ‘fast moving’ components of transport along streamlines and then to update the solution on the grid to account for the ‘residual flux’. This allows us to preserve the speed of streamline simulation while including all relevant physics. The predictor-corrector formulation essentially utilizes the streamline method as a pre-conditioner to finite difference simulation. Our initial experience with the approach has been extremely positive. As an illustration, we have shown below the water-cut response from a dual porosity dual permeability fractured reservoir using the streamline model in a predictor-corrector scheme. We have also shown the response from ECLIPSE. Notice the impact of the corrector-step in converging to the appropriate solution. The corrector step accounts for the cross-flux between the matrix and the fracture system because of the cross-over of streamlines between the systems. We will continue to investigate the role of the predictor-corrector formulation in incorporating additional physics into streamline formulation while retaining the computational advantage. To start with we will include compositional effects into the streamline formulation as a precursor to history matching and calibration of compositional reservoir models.
Comparison between the DPDP streamline simulator and the DPDP ECLIPSE in terms of water cut in the side and corner wells in a homogeneous 5-spot pattern. Notice the huge impact of the corrector step. |
||